探索性分析
在基本完成数据质量的校验之后,接下来我们可以通过查看标签在不同特征上的分布,初步探索哪些特征对标签取值影响较大,以及这些特征是如何影响标签取值的,是后续进行特征工程的重要输入。
首先可以查看一下标签字段的取值分布情况。
本文中绘图代码会尽量使用两种常用的绘图库,Matplotlib和Plotly,分别绘制相似的图表。
Matplotlib是Python中最常用的绘图库之一,它提供了丰富的绘图功能,但美观性和对中文的支持相对较弱。Plotly是一个交互式绘图库,更加现代化,对中文的支持也更好,但代码没有Matplotlib简洁,有一定的学习曲线。
标签分布
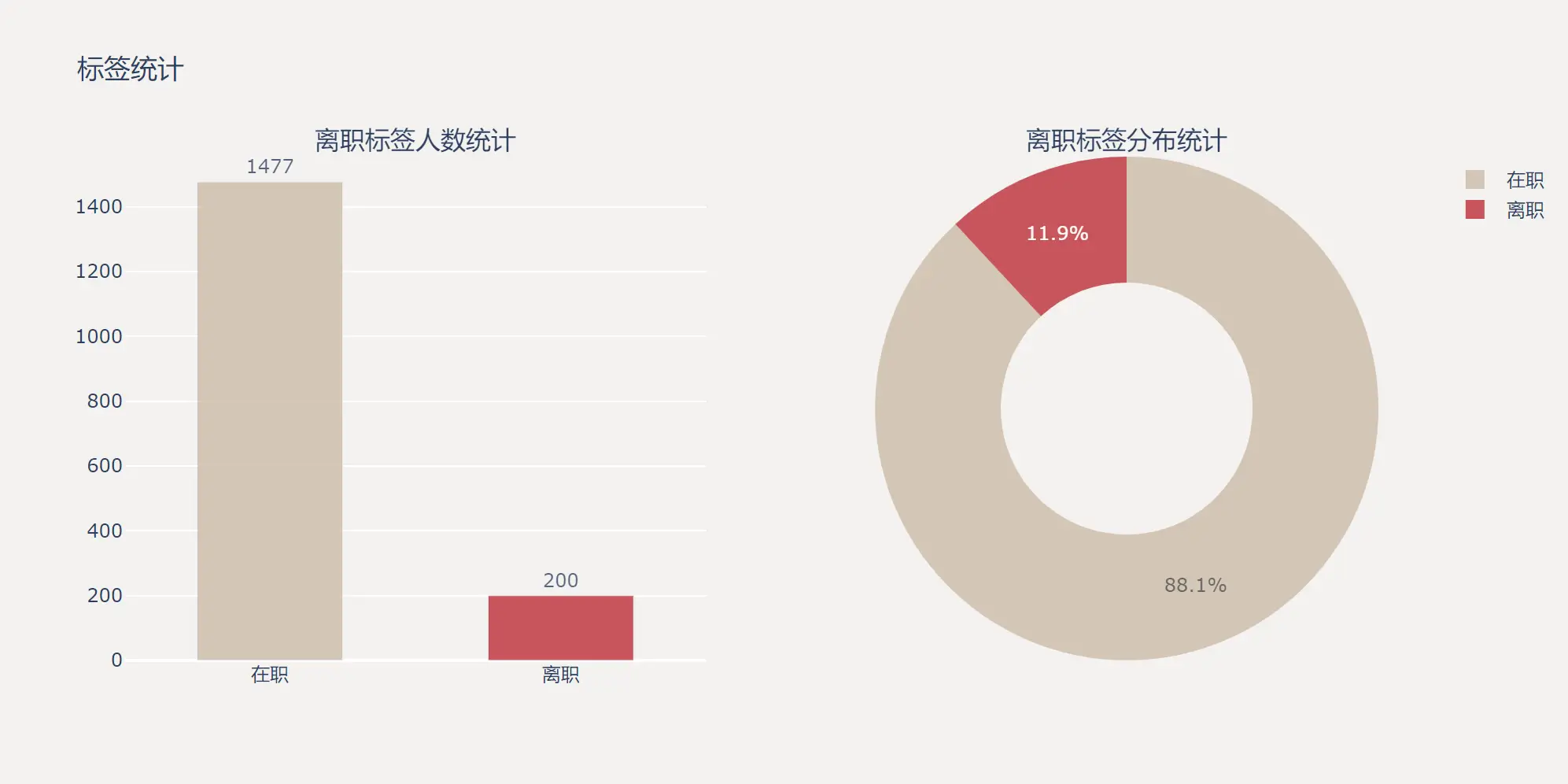
拿到数据集的首要任务就是看一下标签的分布情况,有助于了解标签类别数量以及样本是否平衡等。
柱状图和饼状图是最常用的两种最常用的观测标签分布的图表。
从该数据集的标签分布可以看出,这是一个严重的偏态分布问题,离职的人数远远少于在职的人数。
相关性系数
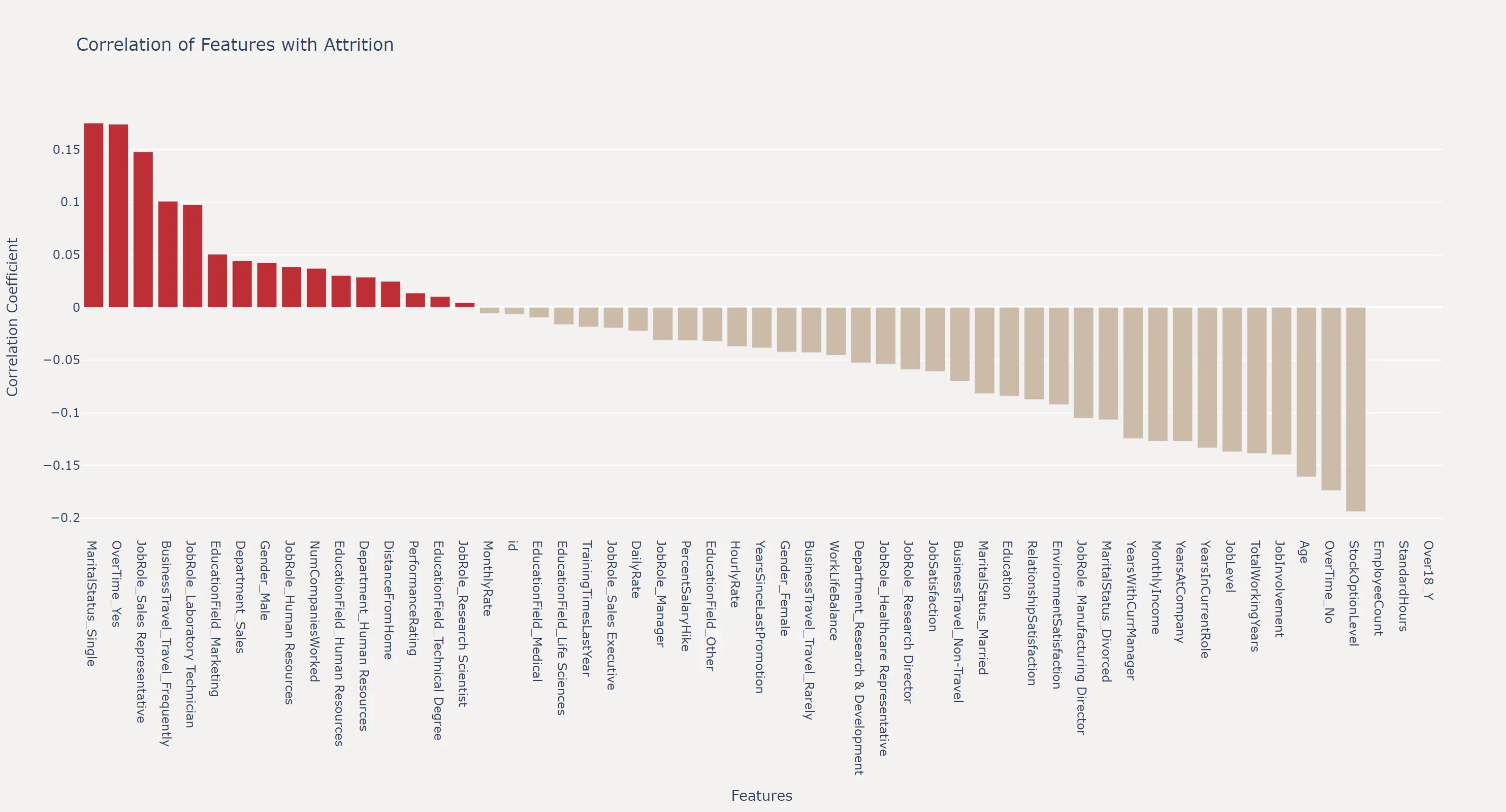
在直观的观察特征在不同标签上的分布情况之前,我们可以先通过计算特征与标签之间的相关性系数来量化特征对标签的影响程度。
在读图时,不仅要关注左侧正相关的特征,也要关注末尾负相关的特征,正负相关都是对标签有重要影响的特征。因此有时也会给相关性取绝对值,来观察特征对标签的影响程度。
连续特征在不同标签上的分布
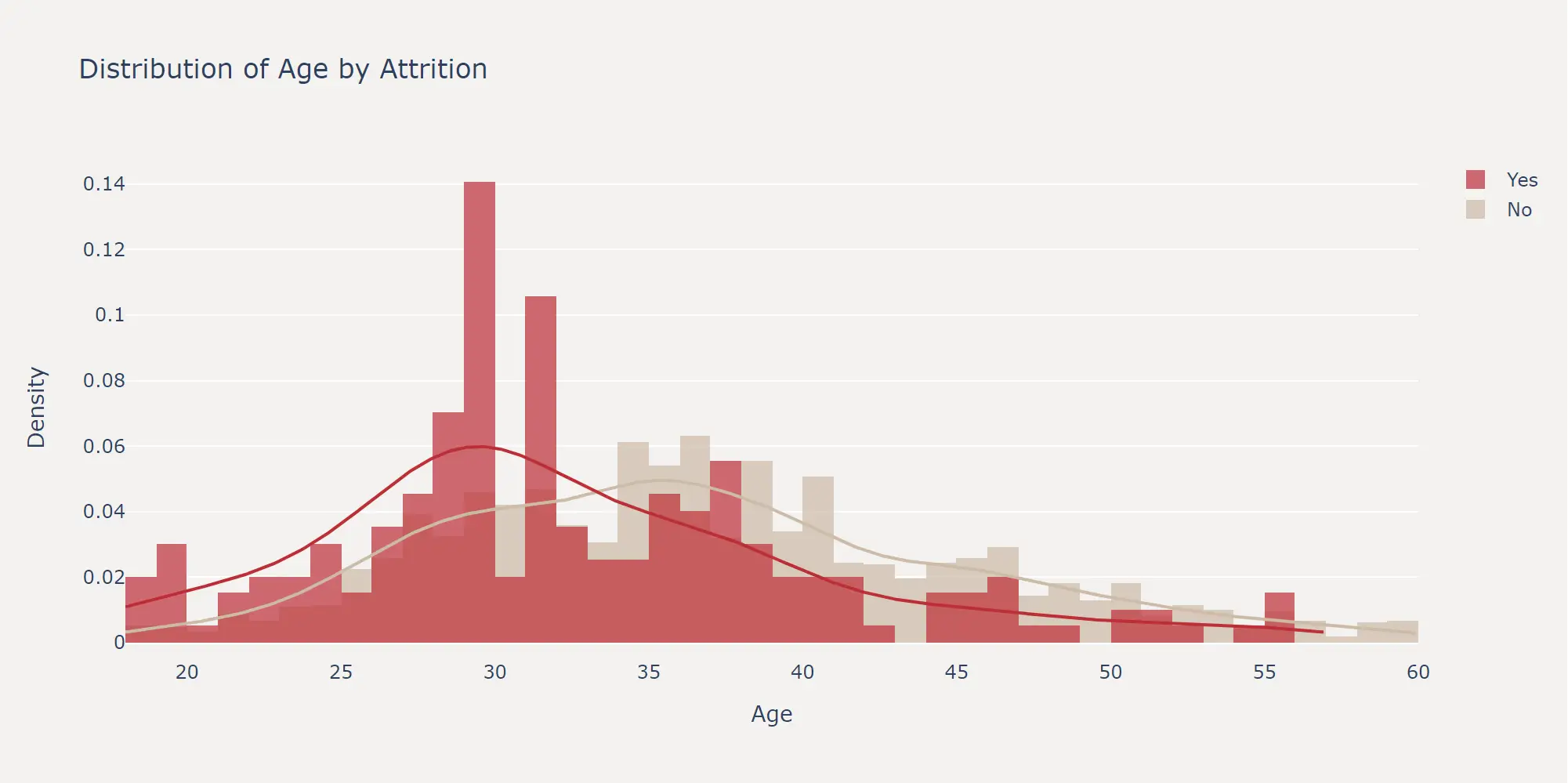
对于连续特征,我们可以通过绘制直方图和核密度估计曲线来查看特征在不同标签上的分布情况。这里以 Age 特征为例,绘制了离职和在职员工的年龄分布图。
可以看出,33岁是一个明显的分界点,在此以下离职均高于在职,反之在此以上在职均高于离职。下一节的特征工程,我们就可以基于该结论,创造一个新的特征是否33岁以上。
这也是对连续特征进行特征工程时,最直观有效的方法。即通过观察特征在不同标签上的分布情况,来确定最佳的分箱点。
可以替换代码中的 feature变量为你感兴趣的特征,或写一个for循环来一次性绘制出所有连续特征的分布图。
离散特征在不同标签上的分布
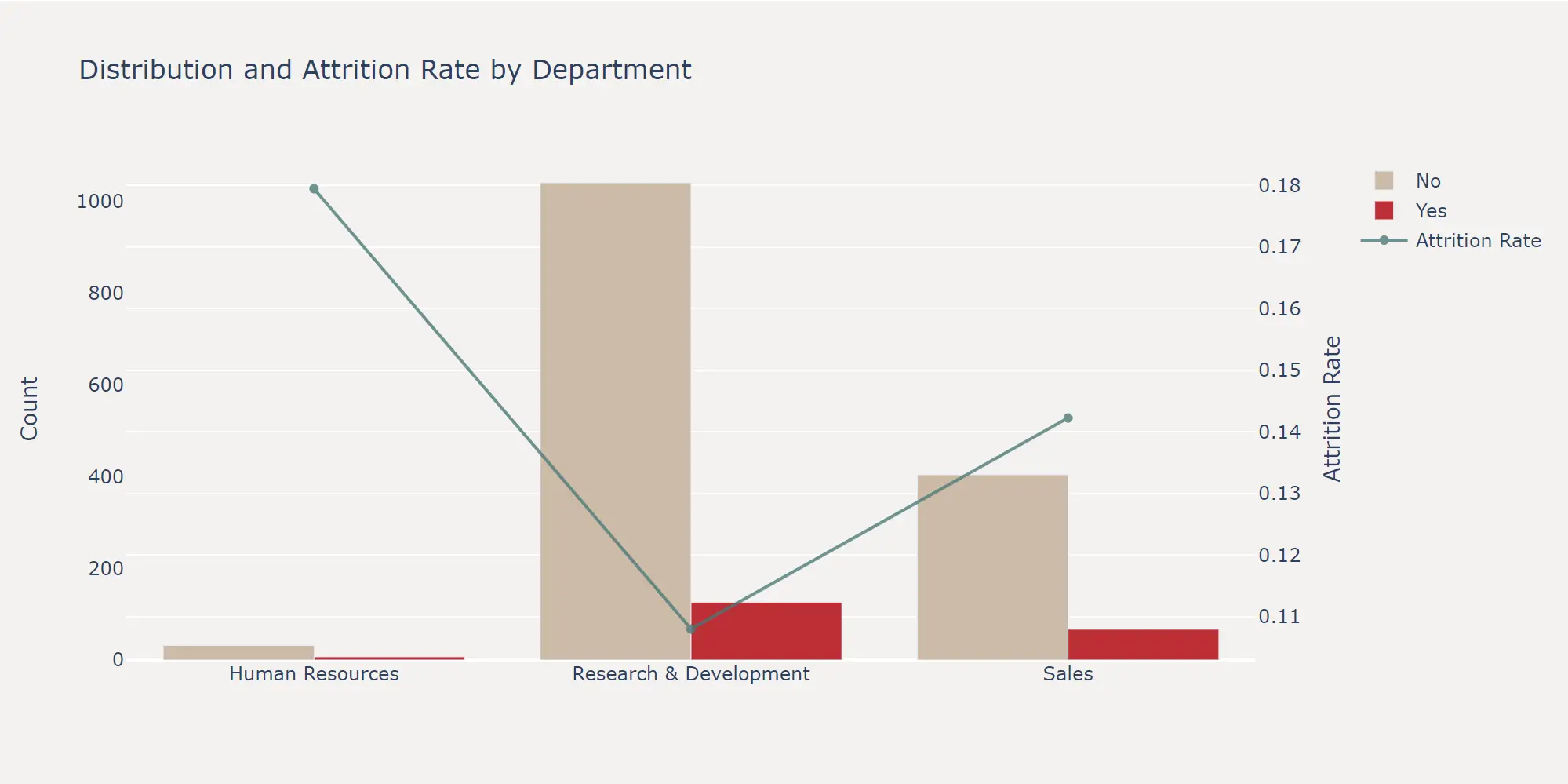
而对于离散特征来说,最有效的观察方式其实就是简单的计算离职率。这里以 Department 特征为例,绘制了各部门的在职和离职人数柱状图,以及离职率折线图。
组合特征在不同标签上的分布
离散特征&连续特征组合
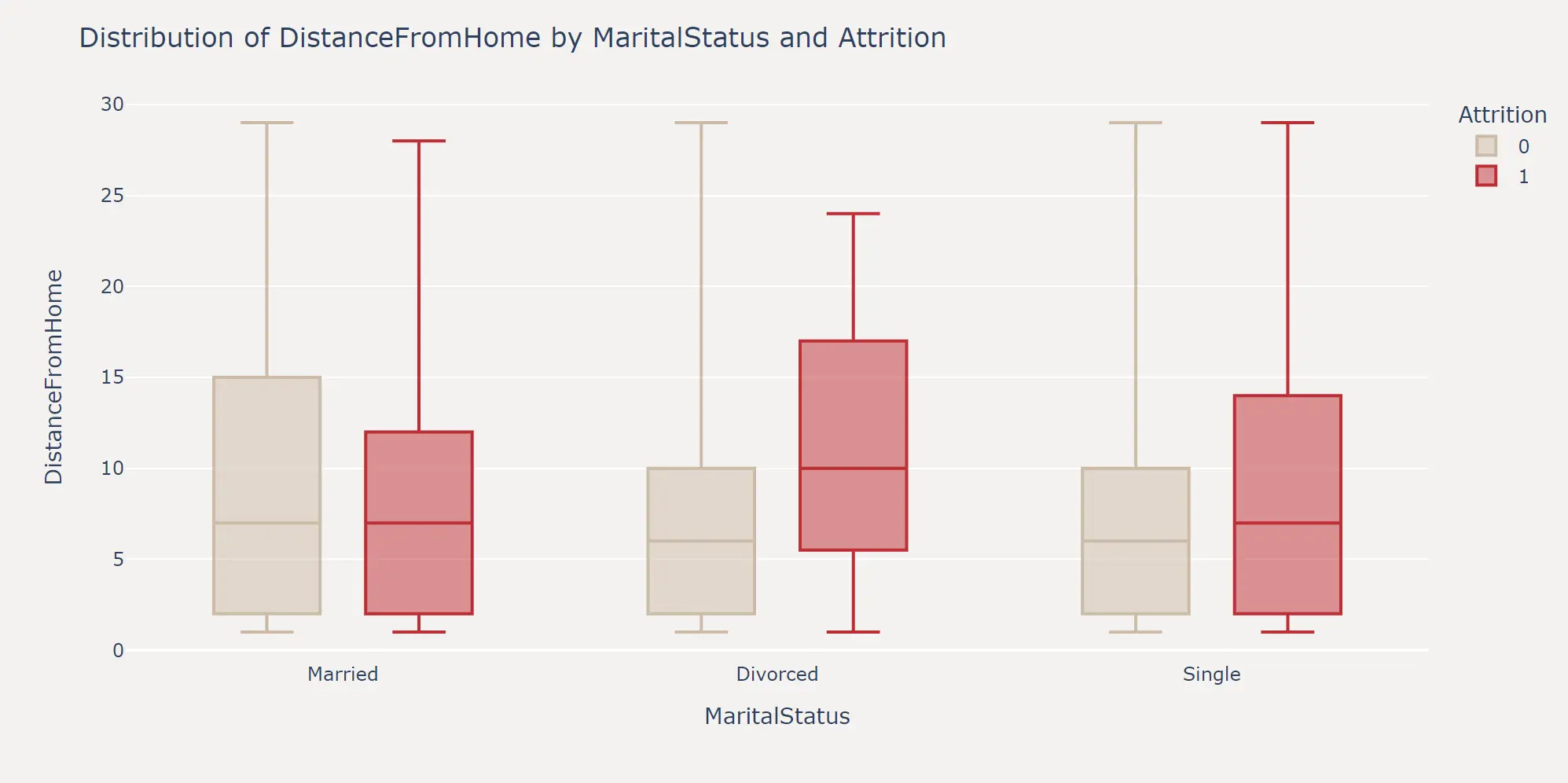
进一步的,我们可以将特征两两结合,探索组合特征在不同标签上的分布情况。这里以 MaritalStatus 和 DistanceFromHome 两个特征为例,绘制了在职和离职员工的 DistanceFromHome 分布箱线图。
可以看出,单身和离异的员工在距离公司较远时有更高的离职概率,在特征工程环节我们依然可以据此来构造新的特征。
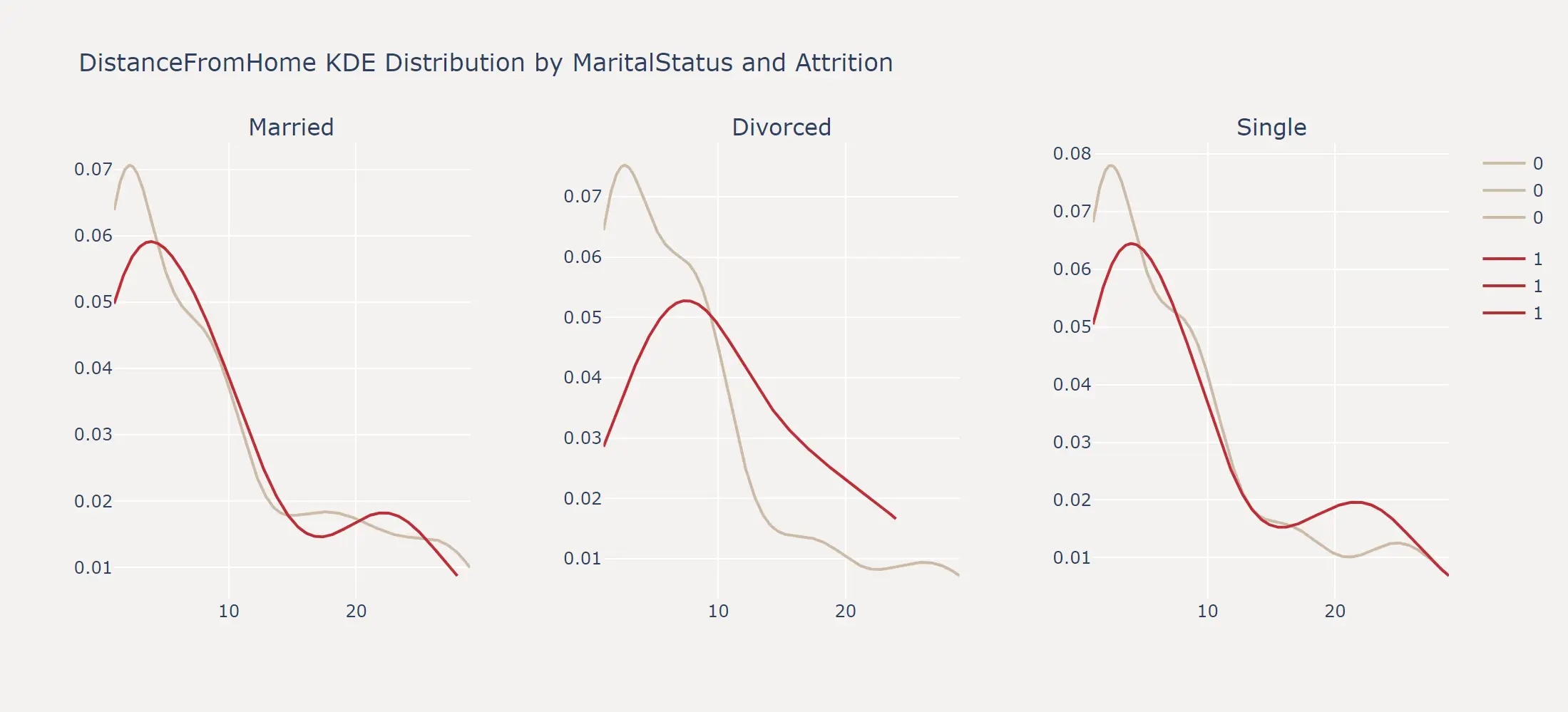
当然,对于连续变量与离散变量组合的情况,我们也可以绘制每个维度下的概率密度曲线。
连续特征&连续特征组合
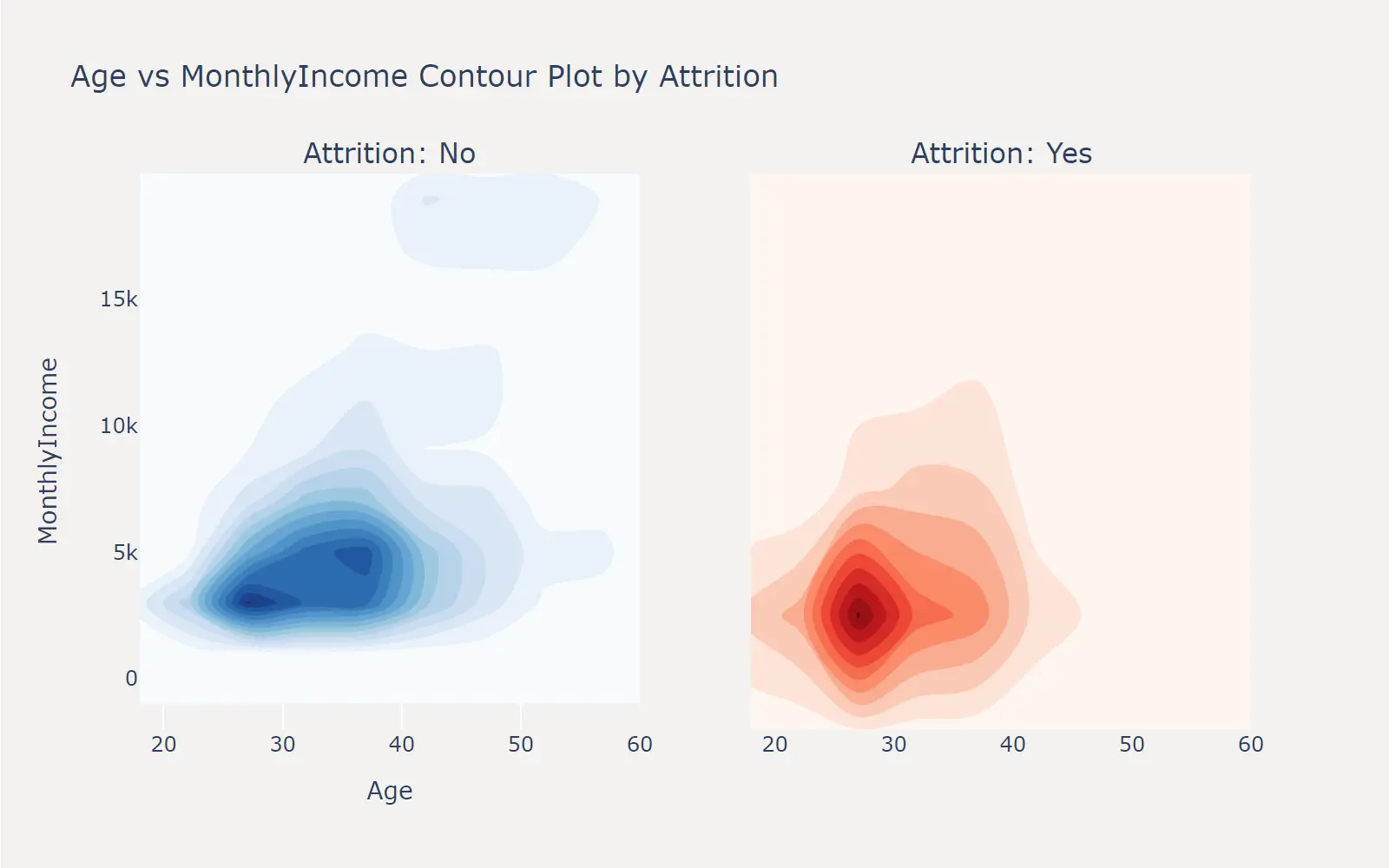
对于两个连续特征的组合,我们可以绘制等高线图来观察两个特征之间的关系。这里以 Age 和 MonthlyIncome 两个特征为例,绘制了在职和离职员工的 Age 和 MonthlyIncome 的等高线图。